考点二、分段函数的奇偶性

解析：分别讨论每一个区间与其对称区间上的对称性，是否符合奇偶性的定义．

例1、判断下列函数的奇偶性：

分析：先验证函数定义域的对称性，再考察

综上可知，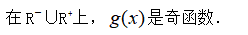

例2、判断函数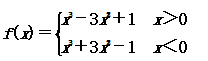)的奇偶性．

     思路点拨：分x＞0或x＜0两种情况计算f(－x)，然后再判断f(－x)与f(x)的关系．

     解：函数f(x)的定义域是(－∞，0)∪(0，＋∞)，关于原点对称．

①当x＞0时，－x＜0，

 则f(－x)＝(－x)³＋3(－x)²－1＝－x³＋3x²－1＝－(x³－3x²＋1)＝－f(x)．

②当x＜0时，－x＞0，

则f(－x)＝(－x)³－3(－x)²＋1＝－x³－3x²＋1

＝－(x³＋3x²－1)＝－f(x)．

由①②知，当x∈(－∞，0)∪(0，＋∞)时，

都有f(－x)＝－f(x)，所以f(x)为奇函数．

【名师点拨】　分段函数的奇偶性应分段证明f(－x)与f(x)的关系，只有当对称的两段上都满足相同的关系时，才能判断其奇偶性．也可根据图象判定．

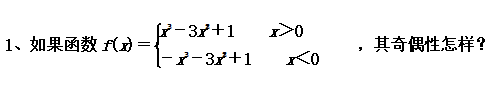
解：当x＞0时，f(x)＝x³－3x²＋1，－x＜0，f(－x)＝－(－x)³－3(－x)²＋1＝x³－3x²＋1＝f(x)．

    当x＜0时，f(x)＝－x³－3x²＋1.－x＞0，f(－x)＝(－x)³－3(－x)²＋1＝－x³－3x²＋1＝f(x)．

    综上可得f(－x)＝f(x)

    ∴f(x)为偶函数．