由偶函数的定义可得：

偶函数的图像关于y轴对称，反过来， 若一个函数的图像关于y轴对称，则这个函数是偶函数.

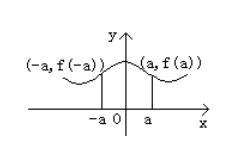
由奇函数的定义可得：

奇函数的图像关于原点对称，反过来， 若一个函数的图像关于原点对称，则这个

函数是奇函数

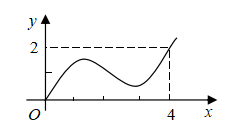
例2．如图，给出了奇函数y = f (x)的局总图象，求f (– 4).

1．奇函数y＝f(x)(x∈R)的图象必过点(　　)

解析：∵f(x)是奇函数，∴f(－a)＝－f(a)，即自变量取－a时，函数值为－f(a)，故图象必过点(－a，－f(a))．

答案：C

2．若函数y＝f(x)是偶函数，其图象与x轴有两个交点，则方程f(x)＝0的所有实根之和是(　　)

    A．2      B．1        C．0       D．－1

解析：∵偶函数图象关于y轴对称，∴f(x)与x轴的两个交点关于y轴对称，若一根为x1，则另一根必为－x1，故f(x)＝0的所有实根之和为0.

答案：C

3．已知f(x)在R上是奇函数，且满足f(x＋4)＝f(x)，当x∈(0,2)时，f(x)＝2x2，则f(7)＝(　　)

   A．－2         B．2      C．－98     D．98

解析：∵f(x＋4)＝f(x)，∴f(7)＝f(3＋4)＝f(3)＝f[4＋(－1)]＝f(－1)．

    又∵f(－x)＝－f(x)，∴f(－1)＝－f(1)＝－2×12＝－2，∴f(7)＝－2，故选A.

    答案：A